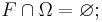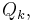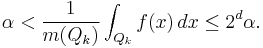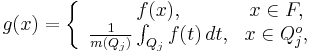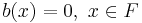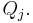Calderón–Zygmund lemma
In mathematics, the Calderón–Zygmund lemma is a fundamental result in Fourier analysis, harmonic analysis, and singular integrals. It is named for the mathematicians Alberto Calderón and Antoni Zygmund.
Given an integrable function 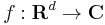 , where
, where 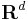 denotes Euclidean space and
denotes Euclidean space and 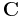 denotes the complex numbers, the lemma gives a precise way of partitioning
denotes the complex numbers, the lemma gives a precise way of partitioning 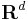 into two sets: one where f is essentially small; the other a countable collection of cubes where f is essentially large, but where some control of the function is retained.
into two sets: one where f is essentially small; the other a countable collection of cubes where f is essentially large, but where some control of the function is retained.
This leads to the associated Calderón–Zygmund decomposition of f, wherein f is written as the sum of "good" and "bad" functions, using the above sets.
Contents |
Calderón–Zygmund lemma
Covering lemma
Let
be integrable and α be a positive constant. Then there exist sets F and
such that:
- 1)
with
- 2)
almost everywhere in F;
- 3)
is a union of cubes,
, whose interiors are mutually disjoint, and so that for each
Calderón–Zygmund decomposition
Given f as above, we may write f as the sum of a "good" function g and a "bad" function b,
. To do this, we define
where
denotes the interior of
, and let
. Consequently we have that
for each cube
The function b is thus supported on a collection of cubes where f is allowed to be "large", but has the beneficial property that its average value is zero on each of these cubes. Meanwhile 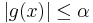 for almost every x in F, and on each cube in
for almost every x in F, and on each cube in  , g is equal to the average value of f over that cube, which by the covering chosen is not more than
, g is equal to the average value of f over that cube, which by the covering chosen is not more than 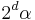 .
.
References
- Stein, Elias (1970). "Chapters I–II". Singular Integrals and Differentiability Properties of Functions. Princeton University Press.